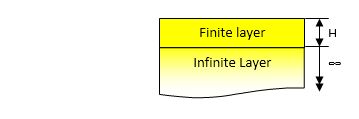
2/15/2017 Topic: Subgrade Characterization Arno Hefer Administrator	When a multi-layered pavement system is set up for modelling using linear elastic mechanistic theory, the last layer of the geometric setup is a semi-infinite half space. Subgrade stiffness varies with depth due to influences such as stress dependency of the material, increased overburden pressure etc. Using a backcalculation routine and assuming a homogeneous semi-infinite subgrade will therefore result in under or over estimation of the stiffness in the critical subgrade zone, just below the pavement structure. Using stiffness values derived from such a model may obviously result in unrealistic pavement responses (stresses and/or stains) obtained during the pavement analysis stage. 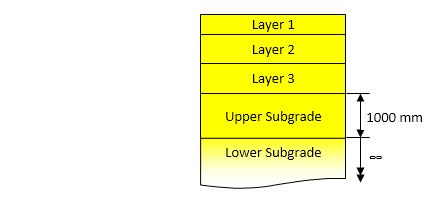The number of available layers in linear elastic programs are normally limited. While many different approaches are used in backcalculation routines in attempts to realistically characterize the subgrade using a limited number of layers, the approach used in Rubicon Toolbox divides the subgrade into two layers, namely, the upper and the lower subgrade as illustrated below. The model allows a maximum of 6 layers (including the upper and lower subgrades). The stiffness result for the upper subgrade serves as an input to the pavement model. The upper subgrade therefore represents the critical subgrade zone just below the pavement structure. This layer should be sufficiently thick to represent the actual subgrade within the zone of wheel load influence, but not too thick as it will then recreate the original problem. A thickness of 800 to 1500 mm, and typically 1000 mm normally works well although features such as the presence of shallow bedrock may influence this choice. It is therefore important to utilise information such as test pit profiles, dynamic cone penetrometer data etc. to check subgrade conditions. A final note of caution. Although the lower subgrade stiffness result is normally omitted from the model setup for pavement design/response analysis (so-called forward calculation), this assumption is valid only when traditional strain-based subgrade failure criteria (or transfer functions) are used. If you are using a deflection based failure criterion, please make sure the exact same model setup used during the backcalculation process is transferred and used in the pavement response analysis. edited by arnoh@icon.co.za on 3/4/2017 edited by on 1/28/2023
2/24/2017 Topic: How to use the LET Standard Axle Design Tool Arno Hefer Administrator	The LET Standard Axle Design Tool allows you to analyse pavement response and expected structural capacity under a user-defined axle load using layered elastic theory. We recommend using the LET Standard Axle Design Tool for routine pavement design and analyses. This may include designing new flexible pavements or flexible pavement rehabilitation design. Getting Started The LET Standard Axle Design Tool is accessed through the Design Tools icon on the Rubicon Toolbox Online Tools. If this is the first time you are using the Online Tools, you will need to set up a project by clicking on Manage Projects and create a new project. Alternatively, you can use an existing project if one has already been created. Before using the LET Standard Axle Design Tool, you may need to check that the correct default Loads and Materials have been selected for your analysis. This can be done by clicking on Settings. The default Loads and Materials can be set as per project requirements. These settings are not fixed and can be changed as and when required. Note that you can add your own customized loads by clicking on Manage Load Setups. The various failure criteria can be viewed by clicking on Criteria. Once you have created a new project or selected an existing project, click on the Design Tools icon and select LET Standard Axle Design from the list of design tools. A LET Standard Axle Analysis page will open. Proceed to complete the analysis, working from left to right. Start by clicking on Load Setup. Note, if loads are not available for selection it means that the default loads have not been setup or selected under Settings. Defining the Pavement Structure The LET Standard Axle Design tool makes provision for handling different pavement behavioral phases. This simplified approach is typically used to model the deterioration of bound (or cohesive) layers; traditionally cement stabilized layers. As an example, consider the following pavement structure with a typical setup based on the South African Mechanistic Pavement Design Method and associated material classes. To define the pavement structure click on Pavement: Phase 1. A default table with five layers will display on-screen, as well as text boxes to input the name of the analysis, a description and notes. The selection of a predefined or default material automatically populates the Thickness, Stiffness, Poisson’s ratio and Transfer Functions (or Failure Criterion) fields from the default database. These default values and Transfer Functions are merely indicative, to provide guidance, and should be assessed carefully and adjusted if needed to reflect the specific project or design conditions. The actual inputs should be relevant to the project under consideration and should ideally be derived from processing of data collected for the project; e.g. stiffness values can be backcalculated from deflection data and substantiated or validated using other data sources such as dynamic cone penetrometer data, density measurements, moisture measurements, and laboratory test data. Note, if the Material Class is changed after finalization of the thickness, stiffness values etc., these values will change to the default values associated with the new material. Also note, if materials are not available for selection it means that the default materials have not been selected under Settings. A Phase 1 Pavement Structure table, containing the basic predefined materials, is shown below. The default Transfer Function (or Failure Criterion) is associated with the selected material, and normally a good start. In many cases, one function up or down is selected to meet the required design reliability. In the screen shot below, Cat B represents Category B according to the South African design method associated with a 90% design reliability. It is also possible to select None, implying that the calculated response is not considered in the structural capacity analysis. This does not, however, mean that the entire layer is ignored. The stiffness contribution to the pavement system is still considered. Once you have changed the default settings to the required project inputs, in Phase 1, proceed with defining Phase 2 of the Pavement Structure or Calculate if the Phase 2 analysis is not applicable. If Pavement: Phase 2 is selected, the input table, for Phase 2, automatically appears with prepopulated data from Phase 1 and you only need to change the properties that will change for Phase 2. This ascertains accuracy and compatibility between the two phases with only minor changes needed to reflect the change(s) in the relevant layer(s). The screen shots below show the Phase 2 pavement structure, with prepopulated values from the Phase 1 example structure inputs, and highlights the changes required for the Phase 2 setup. Analysis and Reporting Once you have completed the Phase 2 setup, click on Calculate to generate the analysis report. An example of the Phase 1 analysis report is shown below. The layer highlighted in red represents the critical layer that dictates the pavement life for the phase under consideration. The screen shot below shows the Phase 2 output. As demonstrated, the analysis for this example indicates failure (cracking) of the asphalt surfacing. In such a case a re-run is typically done, changing the asphalt transfer function for both phases to None, which allows deformation of the structural layers to dictate structural capacity. Note, in this example cracking of the surface only takes place after about 10 years, which is the typical life expectancy of asphalt surfaces due to environmental influences in the region considered. Since the surface can be treated by a mill and replace action, the approach of omitting the asphalt layer from the analysis is valid. Note, for a new analysis, the Save option is initially inactive. Once an analysis is saved for the first time, the save option becomes active. For overwriting an existing saved analysis, click on Save. To save as an alternative analysis, click on Save As. Alternatively you can clone your analysis, from the Online Tools page, and rename it as needed. The report for each phase can be copied to the clipboard by right clicking on the report and selecting Copy image or Save image as. The image can then be inserted into a document of your choice (Word, Excel etc.). edited by on 8/23/2024 edited by on 8/23/2024
6/30/2017 Topic: Backcalculation using Benkelman beam data Arno Hefer Administrator	The Manual Backcalc online tool makes provision for a Benkelman Beam load setup. This process works as follows: Go to Online Tools/ Deflection Analysis/ Manual Backcalc; Download the Template to your computer and populate with the data; In the online tool click on Select Data. Browse and select the data file. You will be prompted to select the data sheet and layer thickness sheet to use; You will be automatically be guided to the Backcalculation Settings window where the appropriate load can be defined. These settings can alternatively be accessed by clicking on the Options button. edited by on 5/20/2021
9/6/2019 Topic: How to use the LET Standard Axle Design Tool Arno Hefer Administrator	An overloading analysis can also be done. Refer to the following LET Axle Spectrum Analysis posts for using real axle load data from weigh-in-motion measurements: How to use the LET Axle Spectrum Analysis Tool How the LET Axle Spectrum Analysis Tool works edited by on 1/21/2023
5/1/2020 Topic: Temperature Correction of Backcalculated Moduli Arno Hefer Administrator	Daily temperature variations occur during deflection surveys, and modulus values determined from backcalculation may therefore exhibit similar trends. While temperature can affect the modulus values of all pavement layers (including unbound layers) stiffness moduli of thick asphalt layers are normally considered for adjustment during routine analysis and design. The adjustment essentially represents normalization of moduli from varying field temperatures to a reference temperature (20 to 25 degrees Celsius) The Rubicon Toolbox backcalculation templates make provision for surface and air temperature data measured at each test location. These temperatures are, however, not used in any calculations but only stored in the template and output files for future reference. The following publications can be used as guidance on temperature corrections of backcalculated pavement layer moduli: - Publication FHWA-RD-98-012. Mechanistic evaluation of test data from LTPP flexible pavement test sections, Vol.1: Final Report. US Department of Transport, Federal Highway Administration. April 1998. - Publication FHWA-RD-98-085. Temperature predictions and adjustment factors for asphalt pavements. US Department of Transportation, Federal Highway Administration. June 2000. edited by Arno Hefer on 5/1/2020
5/1/2020 Topic: Number of layers for analysis Arno Hefer Administrator	The Online Manual and Automated Backcalculation Tools can accommodate a minimum of 3 layers and a maximum of 5 layers - including the upper subgrade but excluding the semi-infinite lower subgrade layer. edited by on 1/30/2023 edited by on 2/2/2023
10/15/2020 Topic: Selection and application of drainage coefficients Arno Hefer Administrator	The AASHTO Structural Number (SN) makes provision for the effects of certain levels of drainage on predicted pavement performance. This is achieved using a drainage coefficient (mi) to modify the layer coefficient (ai) integrated into the SN equation along with the layer thickness (Di) input: SN = a1ˑD1 + a2ˑm2ˑD2 + a3ˑm3ˑD3 The drainage coefficient only applies to the effects of drainage on untreated/natural materials. The designer should assess the level or quality of drainage achieved considering average rainfall and prevailing drainage conditions. The following table contains definitions of drainage levels associated with typical mi ranges as a function of percentage time during a year the pavement structure would approach saturating moisture levels. For comparison purposes, the conditions at the AASHTO Road Test site are considered “Fair” (free water removed within 1 week) with a drainage coefficient of 1.0. 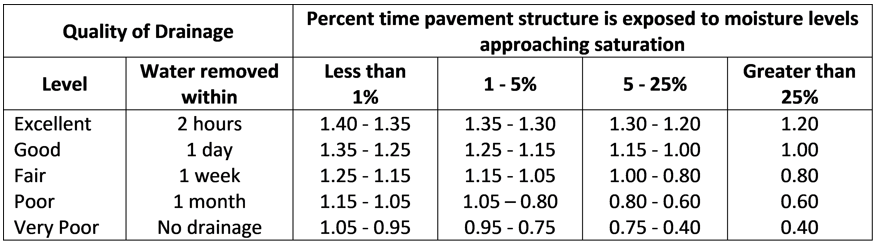Recommended drainage coefficient values for modifying the layer structural layer coefficients of untreated layers in flexible pavements (adapted from AASHTO, 1993) Reference: AASHTO Guide for Design of Pavement Structures (1993). American Association of State Highway and Transportation Officials, Washington, D.C. edited by on 10/21/2020 edited by on 10/17/2023
1/20/2021 Topic: Deflection at the 200 mm offset: Warning Arno Hefer Administrator	The following figure shows a deviation of the measured deflection at the 200 mm offset from the expected deflection bowl (green line). This phenomenon is typically observed in FWD measurements recorded on highly flexible pavements. This error occurs due to the positioning of the sensor at the 200 mm offset close to the edge of the load plate; essentially the result of a stress wave induced by the impact load and non-uniform stress distribution under the relatively rigid load plate, with higher stress intensity towards the plate edge. Recommendations on deflection analysis where deviation of the deflection at the 200 mm offset is present: Deflection bowl parameters: Deflection based parameters that rely on the deflection at the 200 mm offset, such as the Radius of Curvature, should be interpreted and used with caution where this phenomenon occurs. Backcalculation: When fitting the theoretical deflection bowl, the process should focus on the adjacent sensors while ignoring the deflection recorded at the 200 mm offset. edited by on 1/20/2021 edited by on 1/20/2021 edited by on 1/27/2021
4/17/2021 Topic: Evaluation of Backcalculation Results and Errors Arno Hefer Administrator	A question often asked by practitioners is: “What percentage error is acceptable when evaluating backcalculation results?” Backcalculation requires some skill and experience to perform well. The analyst should understand how changes in different layer properties will affect the deflection bowl and should also have good knowledge of material behaviour. With these basic skills, most engineers should be able to obtain useful results from backcalculation analysis; however, without these basic skills the result of a backcalculation analysis can be highly inaccurate, even when there is a seemingly good match between the measured and calculated deflection bowls. Because of this, it is often said that backcalculation is more an art than an exact science. In evaluating the results, not only the precision of fit of the deflection bowl (or percentage error per sensor) but also the reasonableness of the backcalculated stiffness values obtained, should be critically evaluated. Stiffness values should be realistic in terms of prior knowledge of materials (e.g. material class, typical stiffness ranges), visual observations in test pits, other indicators such as Dynamic Cone Penetrometer (DCP) results, etc. For granular (unbound) materials, keep an eye on modular ratios – an unbound material cannot have a stiffness that is higher than about 4 times that of its supporting layer. Whilst the average error per sensor obtained in the bowl matching process is a good indicator of what we are trying to achieve – how effective the pavement model represents the tested pavement structure – proper perspective of the problem should be maintained during the analysis. Ullidtz et al (1987) states: “It is important to realize, however, that layer elastic theory is only a rather poor approximation of the extremely complex conditions of real pavement structures. Most pavement materials will show viscous, visco-elastic and/or plastic deformation under stress, in addition to the elastic deformations. Pavement materials are often inhomogenous, anisotropic and have non-linear stress-strain (or stress-strain rate) relations. Many materials are even particulate, i.e. consisting of discrete particles. Discontinuities, like edges, joints or cracks, are often present and the conditions at the interfaces (rough or smooth) are not well known.” The statement above emphasises that discrepancies between the measured pavement and our theoretical layered elastic model is the reason why we often cannot reduce the error per sensor to perceived levels of acceptability. The ease or difficulty of matching the measured deflection using the theoretical model depends greatly on the composition and characteristics of the pavement under consideration. Situations that tend to be difficult to analyse are: The influence of thin layers (< 75 mm) on the measured deflection is very small or negligible and in effect impossible to backcalculate. Many thin layers, such as bituminous surfaces composed of several layers of different ages/compositions, are often treated as a single layer during analysis. A thin bituminous layer can also be combined with the base thickness during analysis. Try and build a model with fewer thick layers, as opposed to more thin layers – combine layers with similar properties. Thick asphalt layers over strong stabilised (or even concrete) bases, where the asphalt dominates the deflections and it is therefore difficult to determine the effective stiffness of the stabilised subbase. Situations where the subgrade is very stress sensitive – the effective stiffness of the material changes vertically and horizontally and the layered elastic model assuming one uniform subgrade is not suitable. The vertical effect can generally be accounted for by subdividing the subgrade into two or more layers (see Online Help/FWD Analysis/Backcalculation: General/Subgrade Characterization) Pavements exhibiting very high deflections (thin pavements, often with stress sensitive subgrades) result in highly non-linear deflection bowls that are difficult to fit using linear elastic models. In these situations, the geometry and configuration of the FWD device can affect the measurements (e.g. see Online Help: FWD Analysis/ Deflection Analysis/ Deflection at the 200 mm Offset: Warning) In evaluating the backcalculation results, a balance between a good fit and reasonable stiffness results needs to be struck. Whilst an average error per sensor below 2% is exceptional, an error of 5% providing reasonable results may be sufficient. For the outer 3 to 4 sensors, it is usually possible to obtain an error of 0. Note that when the error is less than the precision of the measuring device, 0 error is shown. Generally, for pavements that are difficult to analyse, an average error per sensor of less than 10% may still be acceptable. You should always keep in mind that – in the holistic experienced based approach – that we recommend – the stiffness values obtained from backcalculation are only rough indicators of layer stiffness and condition. We believe that before these stiffnesses are used in design calculations, they should be verified and cross-checked with other test data. Thus, in backcalculation, you should try and establish a habit of focusing on the essential feedback or information that the backcalculation process is giving you. If you can confidently determine the approximate stiffness of each layer, and if you use these to determine if the layer represents the material in question in a very soft, medium stiff, or very stiff condition, then you will have extracted all of the reliable information from your deflection data. (Also see our Online Help/ Design Tools/ DEMAC Materials Classification System) Bibliography Jooste, F.J. 2005. Rubicon Toolbox Technical Support Notes. Modelling and Analysis Systems, Pretoria, South Africa. Rohde, G.T. 1992. Bowler User Guide. Van Wyk & Louw, Pretoria, South Africa. Ullidtz, P., Battiato, G., Larsen, B.k. and Stubstad, R.N. 1987. Verification of the analytical-empirical method of pavement evaluation based on FWD testing. Proc. 6th Int. Conf. on the structural design of asphalt pavements, Ann Arbor, MI, USA. edited by on 4/17/2021 edited by on 4/22/2021
5/4/2021 Topic: Are the 1986 and 1993 versions different? Arno Hefer Administrator	Although the AASHTO design guide has undergone a number of revisions since 1961, practically no difference exists between the basic design methods presented in the 1986 and 1993 versions. Only the 1986 overlay design method was completely revised (essentially simplified) in the 1993 version. Rubicon Toolbox caters for the basic design method and although the AASHTO overlay design procedure does not explicitly feature, the principles outlined in the AASHTO guide can be implemented using the design module.
7/14/2021 Topic: DCP: CBR Relationships Arno Hefer Administrator	Published relationships between DCP penetration rate (or DCP number, DN, with unit mm/blow) and CBR are outlined in the following table. These relationships produce an in situ or field CBR which means that the derived value reflects the CBR of the material at in situ/field moisture and density. edited by on 7/14/2021 edited by on 1/15/2022 edited by on 1/19/2022
1/11/2022 Topic: DCP: Elastic Modulus Relationship Arno Hefer Administrator	This relationship is published in “Use of the Dynamic Cone Penetrometer (DCP) in the Design of Road Structures”, CSIR Research Report DPVT-187, September 1991, by M. De Beer. The relationship was developed from a total of 86 data points where DCP measurements were conducted in parallel with multi-depth deflectometer (MDD) positions on Heavy Vehicle Simulator (HVS) test sections. The Elastic modulus for each pavement layer was backcalculated from layer thickness inputs and in-depth measured deflections using linear elastic theory. The following equation provides the average relationship between DCP penetration rate (DCP Number or DN-value) and effective Elastic Modulus. The following table summarises the confidence interval information for this relationship: edited by on 1/12/2022 edited by on 1/15/2022
1/11/2022 Topic: DCP: Structural Capacity Relationships Arno Hefer Administrator	Estimates based on the DSN800 Parameter A fair estimate of the structural capacity of well-balanced pavements with unbound materials can be obtained with DCP measurements. The empirical relation between the structural capacity and the total number of DCP blows to penetrate 800 mm into the pavement (DSN800) is as follows: Reference: E. G. Kleyn (1984). Aspects of Pavement Evaluation and Design as determined with the Dynamic Cone Penetrometer. M Eng Thesis (in Afrikaans), Faculty of Engineering, University of Pretoria. DCP Penetration Rate - CBR Cover Requirement Relationships The following equation can be used to determine the required DCP penetration rate (DCP Number or DN, mm/blow) at a certain depth within the pavement for an expected future traffic loading demand. Covered required/ depth = 196 x Log(Expected Traffic Load) + 457 x Log(DN) - 1285 The calculated required rate of penetration at a certain depth can then be superimposed on the measured layer-strength diagram. Reference: G. J. Jordaan (1989). Guidelines Towards the Use of a Rehabilitation Design Method Based on Dynamic Cone Penetrometer (DCP) Measurements as Developed in South Africa. Research Report DPVT 43, CSIR, Pretoria. edited by on 1/15/2022 edited by on 1/17/2022 edited by on 1/17/2022
4/1/2022 Topic: The Axle Spectrum Analysis Tool - How it works Arno Hefer Administrator	Principles Accumulated damage is calculated using Miner’s Linear Damage Rule. This rule assumes that damage caused by each load repetition at a given stress level is equal, i.e. the first repetition is as damaging as the last repetition. A portion of the useful life is therefore used up by a number of repeated loads (or stress cycles) at a particular level proportional to the total number of load repetitions allowable (until failure) that can be applied at that particular stress level. The damage ratio (D) is therefore: When 100% of the life is expended, the pavement is expected to fail with D = 1. Since D is dimensionless, this ratio can be calculated and summed for different axle loads (or load groups) applied to the same pavement simultaneously. For the purpose of damage analysis, the sum of the damage ratios for the spectrum of axle loads can be evaluated at predefined periods per year; each year could be considered as one period with the same material properties throughout the year, or the year could be divided into seasons. Application The Axle Spectrum Analysis Tool applies these principles using mechanistic-empirical (ME) analysis using the same LET model and approach built into the Standard Axle Analysis Tool. The pavement structure is specified in exactly the same way. The allowable number of repetitions (to failure) is calculated for each axle load (or load group) for each layer using ME analysis. The specified daily number of repetitions and growth rate(s) associated with each axle load (or load group) is used to calculate the actual number of repetitions accumulated to the end of each period for the load (or group) under consideration. The accumulated damage ratio at the end of each period is calculated for each axle load (or group) and pavement layer. The sum of the accumulated damage ratios across the spectrum of loads (or load groups) at the end of each period is calculated for each pavement layer. The layer with accumulated sum of damage ratios that reaches 1 first, is the critical layer representing failure and the accumulated period represents the pavement life in years. The following schematics present the simplified process of calculating the damage ratios and the life of the critical layer when D = 1. edited by on 4/1/2022 edited by on 4/1/2022 edited by on 4/2/2022 edited by on 4/2/2022
9/15/2023 Topic: Concrete Block Pavement Design Arno Hefer Administrator	The LET Standard Axle Design tool can be used to design concrete block pavements. This can be done by defining the pavement structure using the following typical input assumptions for the paving blocks and bedding sand: Paving blocks: Thickness, Stiffness = 3200 MPa, Poisson’s ratio = 0.3. No failure criterion selected (default NONE under failure criteria drop-down) Bedding sand: Thickness, Stiffness = 200 MPa, Poisson's ratio = 0.35. No failure criteria selected (default NONE under failure criteria drop-down) A standard mechanistic-empirical analysis is then performed with the focus on the behaviour of the supporting structure, i.e., either analysing a layer for deformation or fatigue failure depending on the materials under consideration. Note that as with any layer material defined in a mechanistic-empirical design setup, a proper specification or reference to the standard specification for both the paving blocks and bedding sand is critical to ensure good performance. edited by on 9/18/2023 edited by on 9/18/2023
3/13/2024 Topic: Handling Thick Cemented Layers Arno Hefer Administrator	The question of how to model pavements with cemented layers in Mechanistic-Empirical analyses is often asked, particularly in terms of the thickness of the layers and the phased approach to the analysis. Thickness Considerations Guidance on how to address the issue of two cemented layers in a pavement structure in the South African Mechanistic Design Method (SAMDM) can be found by examining how the Catalogues in TRH4 (1996) were developed. The basis of these catalogues were developed with SAMDM analyses, however the catalogues were calibrated with experience of pavement designs. In the TRH4 (1996) catalogue, some cemented layer thicknesses were combined. For example, 2 x 150mm layers shown as a 300mm layer – typically associated with heavier pavement traffic load classes and higher category roads. The catalogue also includes examples where cemented layers are not combined. When evaluated mechanistically, pavements analysed containing a thick layer (e.g. 300mm cemented) perform better compared to an “equivalent” system incorporating two layers (e.g. 2 x 150mm cemented). Inspection of the catalogue reveals: When there are two layers of the same material (e.g. a C3), a single layer of the combined thicknesses is always used in the analysis of the pavement structure. When there are two layers, but of different materials (e.g. a C3 upper and C4 lower subbase), the layers are analysed separately. Analytical Considerations The SAMDM uses a phased approach associated with the observed performance behaviour of cemented layers. These phases are modelled using different layer moduli. Phase 1 represents an effective fatigue phase, with a higher modulus representative of a lightly stabilised cemented layer. Phase 1 takes the cemented layer from the initial stabilised state to an advanced stage of cracking and the start of what is considered the “equivalent granular state”. Phase 2 follows where the layer is considered to be in the equivalent granular phase (with lower modulus similar to a granular material). It is essential to use both phases in a pavement capacity analysis when a cemented layers is present. In a two-layer cemented system using the phased approach, the modulus of the lower layer (which typically cracks first) is reduced, resulting in a higher strain level at the bottom of the top cemented layer which contributes to a shorter life overall than when a single, thick layer, is analysed. The South African Mechanistic Design Method (SAMDM) uses a shift factor to relate the capacity based on the critical strain level to a capacity representing progression to an advanced state of cracking (“equivalent granular state”, which is simply a modelled state where the layer modulus is equivalent to that of a granular material). The shift factor is a function of layer thickness. This relationship is non-linear between approximately 100mm and 420mm, which means that two 150mm layers deteriorate quicker than one 300mm layer. The shift factor calculation is included in the layer capacity in a Rubicon analysis. Conclusions The structural model assumptions of a single, thick layer versus two separate layers represents two different deterioration mechanisms: A SAMDM analysis that includes two cemented layers of the same material will result in a shorter life (capacity) compared to an analysis of the system with one thick cemented layer. In this case, the catalogues were developed using one single layer. These pavements are typically associated with higher category roads. A SAMDM analysis that includes two cemented layers but of two different material classes, e.g. C3 base, C4 subbase, are analysed as two separate layers. These pavements are typically lighter structures for lower category roads. References: 1. Theyse, H.L. 1995. TRH4 Revision (1995). Phase II: Mechanistic Design Analysis of the Pavement Structures Contained in the TRH4 (1995): Pavement Design Catalogue, Transportek, CSIR, Contract Report I/PA/14/95. 2. TRH4. 1996. Structural Design of Flexible Pavements. Technical Recommendations for Highways. Draft. ISBN 1-86844-218-7. Pretoria. edited by on 3/21/2024 edited by on 4/4/2024 edited by on 6/4/2024 edited by on 6/11/2024
5/22/2024 Topic: RSA Asphalt Fatigue Functions for Thin Surfacings Arno Hefer Administrator	The RSA Asphalt Fatigue Transfer Functions or Failure Criteria published in the 1996 Review of the South African Mechanistic Design Method, are known to be conservative, resulting in unrealistically short fatigue lives. In addition, the available functions are only for conventional unmodified binders, whereas modified binders are now routinely used in asphalt paving. The need for well calibrated conventional and modified asphalt transfer functions have also become critical to assess risks associated with increased loading and tyre pressures. In light of the issues experienced with the 1996 South African asphalt fatigue functions, some international functions have often been used. Three of these typical functions are the Shell, Asphalt Institute and TRRL asphalt fatigue functions. In South Africa, the Shell function with a shift factor of 5 – as calibrated in a previous Austroads design guideline (2001 draft revision of 1992 guide) – has been considered as giving reasonable capacity estimates. Denneman et al. (2011) developed and published basic transfer functions for typical South African asphalt mixes from laboratory fatigue test data as part of the Revision of the South African Pavement Design Method (SAPDM). Hefer and Johns (2023) related these functions to field performance of thin asphalt surfacings and published shift factors that also consider different levels of design reliability. The field data used to calibrate or validate the models are from the South African HMA Performance Database, also developed as part of the SAPDM research projects. Notwithstanding the importance of failure mechanisms related to top-down cracking and complexities introduced by ageing, the focus of the fatigue criteria included here, and their application, is classic mechanistic-empirical design with bottom-up fatigue cracking of thin (<50 mm) asphalt surfacings. The RSA asphalt fatigue failure criteria included in the Rubicon Toolbox database has the following form with constants associated with different reliability levels and shift factors summarised in the table below. Most modified mixes included in the HMA Performance Database were applied as overlays, and mechanistic analysis of these sections consistently gave low tensile strains due to the excellent support. Validation analyses indicated that shift factors approaching 1 relate to approximately 5% cracking. As part of a sensitivity analysis, applying shift factors developed for unmodified asphalt functions to modified asphalt functions produces unrealistically high structural capacities for the modified mixes. These analyses suggested that shift factors for modified mixes should generally be limited to less than 2. The following figure shows relative outputs from different functions, including the original SAMDM AC and Shell functions mentioned above. From the figure it is evident that the Shell (SF=5) function is similar to the Medium Modified asphalt function, which explains why the Shell function has been considered to give reasonable estimates of the fatigue life of asphalt layers. References: 1. Denneman, E., Anochie-Boateng, J., Ngapele, M., and Komba, J. (2011). 10th Conf. on Asphalt Pavements for Southern Africa (CAPSA). Champagne Sports Resort, KwaZulu-Natal, South Africa, 11-14 September 2011. 2. Hefer, A. and Johns, F. (2023). 13th Conf. Asphalt Pavements in Southern Africa (CAPSA). Champagne Sports Resort, KwaZulu-Natal, South Africa, 15-18 October 2023. edited by on 5/22/2024 edited by on 5/23/2024 edited by on 5/27/2024 edited by on 6/4/2024 edited by on 6/11/2024
26 days ago Topic: Design using Geosynthetics in Granular Materials Arno Hefer Administrator	The Rubicon Toolbox suite of Layered Elastic Theory (LET) Tools can be used effectively to incorporate design with geosynthetics, using concepts universally accepted in this industry. This overview mainly deals with the use of geosynthetics in granular and/or subgrade layers. The term stabilisation goes beyond just chemical stabilisation or the mechanical blending of different natural materials – it also includes the use of geosynthetics to enhance the structural performance of pavements. The background presented is largely obtained from Hefer et al (2023). Asphalt reinforcement is not included here; for more information, consult other sources such as the South African Sabita Technical Guideline on Asphalt Reinforcement (TG3). Mechanisms For geogrids, the stabilisation effect occurs through internal confinement – interlock of the aggregate with the grid enhances both shear strength and stiffness which propagates into the layer. This is achieved by introducing tensile stiffness at the base of the layer using a suitable planar geosynthetic system. Two key mechanisms contribute to this effect: interface friction and interlocking. While friction can occur between geotextiles and aggregate, interlocking is unique to the interaction between geogrids and aggregate, as the grid structure physically engages with the aggregate particles, preventing their lateral movement and improving the overall stability of the layer. Both the properties of the geogrid and characteristics of the aggregate influence the level of confinement achieved. Key geogrid factors that affect the interaction between geogrid and aggregate include: Aperture size in relation to aggregate size and grading Aperture shape Rib shape and stiffness Stiffness of the junctions between ribs Beyond these geogrid-related factors, the shear properties of the aggregate also play a role in determining the effective thickness of the confinement zone within the layer. To select the optimum aperture size, designers often refer to the maximum aggregate size or a specific sieve size. Research indicates that the maximum geogrid-aggregate interaction is achieved when the aperture size (S) is approximately two to three times the median aggregate size (D50) as shown in Figure 2. Table 1 can be used as a guide for selection of geogrid aperture sizes compatible with different gradations. Research based on a maximum aggregate size of 31.5 mm shows that the following assumptions can be made regarding the height of the full confinement (Vega et al, 2018): Flexible geogrids: Two to three times the maximum aggregate size Rigid geogrids: Four to six times the maximum aggregate size Dissipation of confinement: Over a zone of four to five times the maximum aggregate size For stiff geocells, the stabilisation effect is achieved through external confinement – lateral and shear restraint is facilitated by a three-dimensional matrix of interconnected cells, which imparts tensile stiffness to the unbound layer. The external confinement of the granular infill within the geocell structure further enhances the stiffness of the layer and effectively limits or prevents deformation of the stabilised material. The properties of geocell material directly influence both the immediate confinement achieved and the long-term performance of the system. The key material properties that ensure effective confinement include: High dynamic tensile stiffness of the cell walls Resistance to permanent deformation over time High tensile strength The confinement effect can be assumed to be equal to the cell height as a minimum – due to the spread of the confinement effect, an additional 20 mm of full confinement is generally assumed above the cell (and below, depending on placement). Beyond the fully confined zone, the interlocking effect diminishes over a distance of six to eight times the maximum aggregate size from the top of the geocell. While the quality of the infill material affects the level of modulus improvement, the 3D confinement provided by the geocell allows for the use of a broad range of granular materials, from marginal to high-quality​ Concepts of Improvement Factors The use of improvement factors is widely accepted and caters for implementation using mechanistic-empirical pavement design methods. These factors quantify the improvement of a material or layer quality facilitated by the inclusion of geosynthetics – and is typically expressed in terms of a ratio of the material property (such as modulus) before and after improvement. Suppliers have developed graphs such as the one shown in Figure 4 to determine improvement factors for different geosynthetic products. Relationships typically include the original material quality, geosynthetic properties, and supporting conditions. The generalised example relationships shown below were produced from interpolation between data published for various biaxial polypropylene extruded grids of different strengths, assuming good interlock through aggregate-geogrid aperture/opening size compatibility. ​ Due to the popularity of the AASHTO (1986/1993) empirical pavement design method in the latter half of the 20th century many efforts to develop these factors focused on parameters compatible with this method, notably the Layer Coefficient Ratio (LCR) – defined as the ratio between the layer coefficient of the geosynthetic stabilised layer to the layer coefficient of the original/unstabilised layer. Functions are available to relate the layer modulus with the layer coefficient, and can be used for conversion. Figure 5 shows an example relationship developed for stiff geocells manufactured with novel polymer alloys (NPA). The concept is the same as for LCR but defined in terms of improvement of the material/layer modulus – the Modulus Improvement Factor (MIF). The MIF is defined as the ratio of the modulus of the layer incorporating the geosynthetic, to the modulus of the layer without the geosynthetic. As shown in Figure 5, the MIF in the geocell example is a function of the modulus of the original/infill material and the modulus of the support. The MIF can be implemented for any layer in the pavement structure, but since it implicitly depends on the modulus of the support, this modulus should represent a modulus equivalent to the modulus of a subgrade, i.e. a semi-infinite half-space. While the improvement factors LCR and MIF implicitly consider the support, the resulting modular ratio still needs to be checked for reasonableness. The Improved Modulus Ratio (IMR) is based on the full semi-infinite support. IMR = Es/Esup Where IMR is the Improvement Modulus Ratio, Es the elastic modulus of the geosynthetic stabilised layer, and Esup the semi-infinite modulus (or equivalent) of the supporting layers. A maximum ratio of 5 for geogrid stabilised layers is proposed based on the maximum value known for granular materials (Giroud and Han, 2004). For novel polymer alloy (NPA) stiff geocells, a maximum ratio of 7.6 is proposed (Pokharel, 2010). Design Implementation See the post How To Use The LET Standard Axle Design Tool for mechanistic-empirical design using Rubicon Toolbox. The recommended procedure for incorporating geosynthetics into the design process is outlined in the following figure. This method applies to both granular base and subbase materials, as well as selected gravel and subgrade layers. It is essential to carefully select the geosynthetic based on its intended function and appropriate specifications. For effective design, it is crucial that geogrids or geocomposites are compatible with the natural materials being used to ensure aggregate interlock. Additionally, the confinement thickness or effective thickness must be established as an input for the model, as discussed above. If the final layer thickness surpasses the effective confinement height, two layers may be considered where practical, or the equivalent modulus concept can be applied to combine them into one layer. The latter approach is often necessary when the maximum number of layers is exceeded. The recommended approach for designing geosynthetic-stabilised pavements is to first conduct a full failure analysis without the inclusion of geosynthetics, which serves as baseline/reference design. Once an appropriate geosynthetic product has been selected, considering all relevant specifications and design factors, it can be reasonably assumed that stabilisation will enhance the shear properties within the confinement zone as discussed above, and the effective height of confinement can be determined. In setting up the pavement structural model, therefore, only the increase in stiffness needs to be accounted for in the final design and current practice suggests that failure analysis for the stabilised layer can be excluded. A description of the type of geosynthetic and key properties can be included when setting up the pavement structure in Rubicon Toolbox by adding a User Defined Material – See the post Adding Materials. Design Example In this example, the South African Mechanistic Design Method (SAMDM) and associated material classes are used. 1. Benchmark Design 2. Design with Geosynthetics In this analysis the cement stabilised subbase is replaced with a stiff NPA geocell stabilised subbase. Assume that G7 quality material is available as an infill material. An elastic modulus of 120 MPa is typically associated with this material type. An equivalent semi-infinite elastic modulus of 82 MPa is calculated for the two layers supporting the cemented layer in the original design. Equivalent modulus estimates can be obtained using classic techniques such as Palmer and Barber (1940), or simply selecting an equivalence criterion (such as deflection) and calculating the equivalent/combined modulus through an iterative process using the LET Standard Axle Design Tool or the LET Stress Strain Calculator available in your Rubicon Toolbox. A valid modulus improvement factor (MIF) and maximum improved modulus ratio (IMR) is obtained from the supplier related to the product material specifications. In this example Figure 5 was used; having established the unstabilised modulus Eu of 120 MPa and modulus of the support (Esup) of 82, the resulting MIF ≈ 3.5. The modulus of the geocell stabilised material, Es = MIFˑ Eu = 420 MPa The improved modular ratio (IMR) is Es/Esup = 5.8 which is less than the maximum value of 7.6 associated with stiff geocells. An improved modulus of 420 MPa is therefore accepted. It should be noted that, while an improvement in the granular base modulus can be expected and incorporated due to the support provided by the stiff geocell-stabilised subbase layer (with an improved modulus of 420 kPa), an increase in the shear strength of the granular base material should also be considered. This involves selecting appropriate shear parameters as part of the granular failure criterion inputs. The analysis using the LET Standard Axle Analysis Tool including a stiff NPA geocell is shown below. An NPA geocell with 150 mm thickness and 30mm G7 overfill is recommended resulting in a subbase layer with total thickness of 180 mm. References Cook, J. and Horvat, F. (2014). Assessment of particle confinement within a mechanically stabilised layer. 10th Int. Conference on Geosynthetics (ICG), 21-25 September 2014, Berlin, Germany. Giroud, J.P. and Han, J. (2004) Design method for geogrid-reinforced unpaved roads – Part II: Calibration and verification. ASCE Journal of Geotechnical and Geo-environmental Engineering, 130(8), 787-797. Hefer, A.W., Zannoni, E. and Du Preez, H. (2023). Pavement Design with Geosynthetics. Proc. 13th Conf. on Asphalt Pavements for Southern Africa, 15-18 October 2023, Champagne Sports Resort, KZN, South Africa. Palmer, L.A. and Barber, E.S. (1940) Soil displacement under a circular loaded area. Proceedings, Highway Research Board, Vol 20.Pokharel, S.K. (2010) Experimental Study on Geocell-reinforced Bases under Static and Dynamic Loading. PhD Dissertation. Civil Environmental and Architectural Engineering and Graduate Faculty of the University of Kansas, USA. Mulabdić, M. and Minažek, K. (2012) Nature of friction between geogrids and soil. 5th European Geosynthetic Congress, Valencia, Vol 5, pp. 435 – 440. Mulabdić, M., Minažek, K. and Kaluder, J. (2018) Geogrids – what is important. Certa 2018, 5th Int. Conference on Road and Rail Infrastructure, 17-19 May 2018, Zadar, Croatia. Vega, E., van Gurp, C. and Kwast, E. (2018) Geokunststoffen als funderingswapening in ongebonden funderingslagen. SBRCURnet (CROW), Delft, Netherlands. Zannoni, E. (2016) Geosynthetics – from product to technology in road rehabilitation. Civil Engineering, April 2016, pp. 31-35. Palmer, L.A. and Barber, E.S. (1940) Soil displacement under a circular loaded area. Proceedings, Highway Research Board, Vol 20. edited by on 10/29/2024 edited by on 10/30/2024 edited by on 11/1/2024 edited by on 11/6/2024 edited by on 11/7/2024 edited by on 11/8/2024

---